java写题大模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import java.util.*;
import java.io.*;

import static java.lang.System.out;


public class Main {
    static Scanner in = new Scanner(System.in);
    static int N = (int)(1e5+10);


    public static void main(String[] args) {
        //编写代码段

        in.close();
        out.flush();
    }
}


快读模板

1
2
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
   static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

前缀和和差分（区间加减问题）

image-20250313160104419

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int n = scan.nextInt();
        int q = scan.nextInt();

        int[] a = new int[n];
        int[] pre = new int[n + 1];

        for(int i = 0 ; i < n ; i ++){
          a[i] = scan.nextInt();
        }
        for(int i = 1 ; i <= n ;i++){
          pre[i] = pre[i - 1] + a[i - 1];
        }
       
        int l = 0,r = 0;
        
        for(int i = 0 ; i < q; i ++){
          l = scan.nextInt();
          r = scan.nextInt();
          System.out.println(pre[r] - pre[l - 1]);
        }
        scan.close();
    }

   
}

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class main{
	public static void main(String[] arg){
    Scanner scan = new Scanner(System.in);
    
  }
  
  public static void prefixSum(int l){
    //加一是为了让其与数组一致 一般把0舍弃了 如果不舍弃 java会数组报错,cpp这个pre[0-1]虽然不会报错，但是有隐患 比如说pre[1]就是 a[0]的和，pre[2]就是a[0] + a[1]的和 以此类推
    int[] pre = new int[l + 1];
    //构建前缀和数组
    for(int i = 1 ; i <= n ; i ++){
      pre[i] = pre[i-1] + a[i-1];
    }
  }
}

差分就是前缀合的逆运算：同样也是构筑前缀和数组

Pre[i] = a[i] - a[i - 1];

从差分数组还原原数组：对差分数组求前缀和就是原数组

  • 快速区间修改

​ 通过调整差分数组可以高效完成原数组的区间操作。

​ 对区间[l,r]的每个元素加上一个d，只需要：

​ b[ l ] += d , b[r + 1] -=d.

​ 在完成所有修改后，通过对差分数组求前缀和即可得到最终的结果数组

-

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import java.util.Arrays;
import java.util.Scanner;

//若题目中出现 在什么区间内加或者减数组啥的  可以考虑用差分数组
//差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();+
        int m = scanner.nextInt();
        int[] a = new int[n + 1];
        //比较前缀和  我的模板是从1开始的 ， 而前缀和是从0开始的
        for (int i = 1; i <= n; i++) {
            a[i] = scanner.nextInt();
        }

        // 差分数组
        int[] firr = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            firr[i] = a[i] - a[i - 1];
        }
        
        for (int i = 0; i < m; i++) {
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            int d = scanner.nextInt();
            firr[l] += d;
            // 这里为啥要这么写？ 如果r+1大于n 就不用管后面的内容了
            if( r + 1 <= n){
                firr[r + 1] -= d;
            }
        }
 
        int[] ans = new int[n+1];
        for (int i = 1; i <= n; i++) {
            ans[i] = ans[i - 1] + firr[i];
        }

        for (int i = 1; i <= n; i++) {
            System.out.print(ans[i] + " ");
        }

        scanner.close();
    }
}

二维前缀和和差分

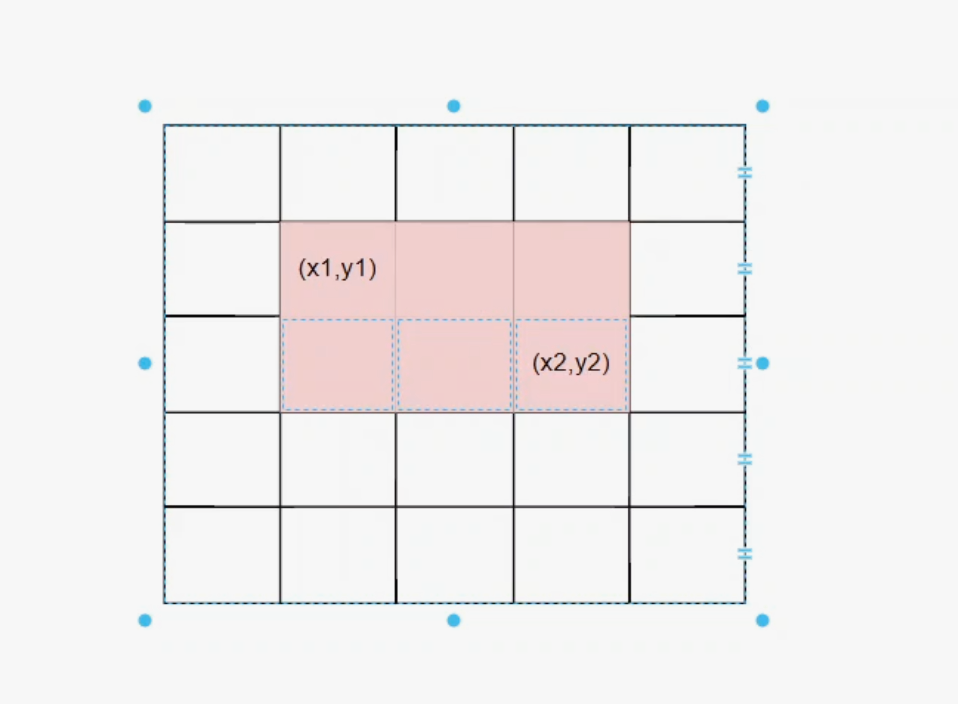
image-20250313192456829

image-20250313192543261

二维前缀和表示的其实是(a,b)到(x,y)的子矩阵的和

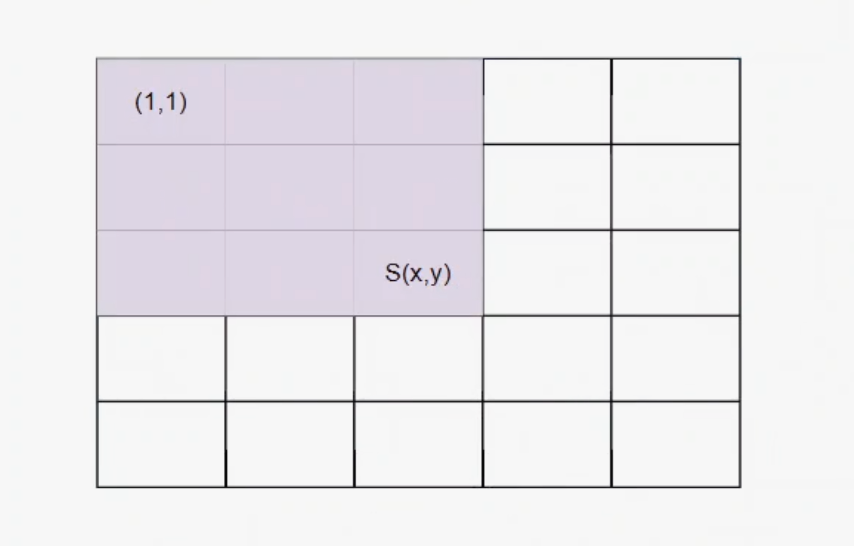
image-20250313193333221

二维前缀和

前缀和数组公式：s(x2,y2) = a(x2,y2) + s(x2,y2-1) + s(x2-1,y2) - s(x2-1,y2-1)

区域公式：s(x1,y1) - > s(x2,y2) = s(x2,y2) - s(x2,y1 - 1) - s(x1 - 1 , y2) + s(x1-1,y1-1)

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import java.util.*;
import java.io.*;
import static java.lang.System.out;

/**
 * @Date: 2025/03/13
 * @Author: Wislist
 **/
public class Main {
    static Scanner in = new Scanner(System.in);
    static int N = (int)(1e5+10);

    static int[][] A;
    static int[][] forMax;
    public static void main(String[] args) {
        //编写代码段
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();
        A = new int[n + 1][m + 1];
        forMax = new int[n + 1][m + 1];
        for(int i = 1 ; i <= n ; i ++){
            for(int j = 1; j <= m ; j++){
                A[i][j] = in.nextInt();
                if(i ==  1 && j == 1){
                    forMax[1][1] = A[1][1];
                }else{
                    forMax[i][j] = A[i][j] + forMax[i][j - 1] + forMax[i - 1][j] - forMax[i - 1][j - 1];
                }
            }
        }


        for(int i = 0 ; i < q ; i ++){
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();
            out.println(forMax[x2][y2] - forMax[x1 - 1][y2] - forMax[x2][y1 - 1] + forMax[x1 - 1][y1 - 1]);
        }

        in.close();
        out.flush();
    }
}

二维差分

前缀和数组求差分后是原数组，原数组求差分后是差分数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import java.util.Scanner;

import static java.lang.System.out;

public class Difference_2D {

    static Scanner in = new Scanner(System.in);

    static int N = (int) (1e3 + 10);
    static int[][] a = new int[N][N];
    static int[][] b = new int[N][N];
    static int[][] ans = new int[N][N];
    static int n,m,q;
    public static void main(String[] args) {
        n = in.nextInt();
        m = in.nextInt();
        q = in.nextInt();

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                a[i][j] = in.nextInt();
                b[i][j] = a[i][j] - a[i - 1][j] - a[i][j-1] + a[i - 1][j-1];
            }
        }

        while(q-->0){
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();
            int d = in.nextInt();
            b[x1][y1] += d;
            b[x2+1][y1] -=d;
            b[x1][y2+1] -=d;
            b[x2+1][y2+1] +=d ;
        }

        for(int i=1;i<=n;i++){
            for(int j = 1 ; j<=m;j++){
                ans[i][j] = b[i][j] + ans[i-1][j]  + ans[i][j-1] - ans[i-1][j-1];
                out.print(ans[i][j] + " ");
            }
            out.println();
        }


    }
}

二分法（分治思想的特殊情况）

哈希表

数组 set map

字符串

kmp算法(匹配字符串问题)

image-20250314090356010

文本串：aabaabaaf

匹配串：aabaaf

暴力匹配：O(m*n)

kmp算法： 前缀表（a,aa,aab,aaba,aabaa）后缀表(f,af,aaf,baaf,abaaf)

最长公共前后缀
(a,aa,aab,aaba,aabaa,aabaaf)
(0, 1 , 0 , 1 （a 一个相等的前后缀） , 2(aa两个相等前后缀) , 0)

1

二叉树

1、遍历

层序遍历：

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
 //从上到下
 public List<List<Integer>> levelOrder(TreeNode root) {
   
   			List<List<Integer>> res = new ArrayList<>()；
        if (root == null) return;
        Queue<TreeNode> que = new LinkedList<TreeNode>();
   			//
        que.offer(node);

        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();

            while (len > 0) {
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);

                if (tmpNode.left != null) que.offer(tmpNode.left);
                if (tmpNode.right != null) que.offer(tmpNode.right);
                len--;
            }

            res.add(itemList);
        }
   return res;
}




//自底向上
class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        // 利用链表可以进行 O(1) 头部插入, 这样最后答案不需要再反转
        LinkedList<List<Integer>> ans = new LinkedList<>();

        Queue<TreeNode> q = new LinkedList<>();

        if (root != null) q.offer(root);

        while (!q.isEmpty()) {
            int size = q.size();

            List<Integer> temp = new ArrayList<>();

            for (int i = 0; i < size; i ++) {
                TreeNode node = q.poll();

                temp.add(node.val);

                if (node.left != null) q.offer(node.left);

                if (node.right != null) q.offer(node.right);
            }

            // 新遍历到的层插到头部, 这样就满足按照层次反序的要求
            ans.addFirst(temp);
        }

        return ans;
    }

补充： morris遍历 时间复杂度为O(1) 在不使用栈或者递归的情况下实现中序遍历。核心思想是利用树中的空闲指针来临时存储信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class MorrisTraversal {
    public void inorder(TreeNode root) {
        TreeNode current = root;

        while (current != null) {
            if (current.left == null) {
                // 如果当前节点的左子节点为空，访问当前节点并移动到右子节点
                System.out.print(current.val + " ");
                current = current.right;
            } else {
                // 找到当前节点左子树的最右节点
                TreeNode predecessor = current.left;
                while (predecessor.right != null && predecessor.right != current) {
                    predecessor = predecessor.right;
                }

                if (predecessor.right == null) {
                    // 如果前驱节点的右子节点为空，将其右子节点设置为当前节点
                    predecessor.right = current;
                    current = current.left;
                } else {
                    // 如果前驱节点的右子节点为当前节点，恢复树的结构并访问当前节点
                    predecessor.right = null;
                    System.out.print(current.val + " ");
                    current = current.right;
                }
            }
        }
    }

反转二叉

其实是左右对称 将左子树反转到右子树上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) return root;
        
        TreeNode node = root.right;
        root.right = root.left;
        root.left = node;
        
        invertTree(root.right);
        invertTree(root.left);
        return root;

    }
}

2、对称二叉

判断是否为对称二叉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public boolean isSymmetric(TreeNode root) {
        boolean isSame = compare(root.left,root.right);
        return isSame;
    }
    boolean compare(TreeNode left , TreeNode right){
        if(left == null && right != null) return false;
        else if(left != null && right == null) return false;
        else if(left == null && right == null) return true;
        else if ( left.val != right.val) return false;

        boolean outside = compare(left.left, right.right);
        boolean inside = compare(left.right, right.left);
        return outside && inside;
    }
}

image-20250313000443450

image-20250313000504570

image-20250313000538381

image-20250313000616084

image-20250313000631763

image-20250313000712655

image-20250313000730596

image-20250313000744133

image-20250313000807006

image-20250313000820935